임민석의 블로그

처음엔 1, 11, 111... 이런식으로 수를 늘려가면서 수를 나눠본 후, 처음 나누어 떨어졌을 때의 자리수를 구하면 된다고 생각했다. 코드는 아래와 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringJoiner;

public class Main {
    public static void main(String[] args) throws IOException {
        final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        final StringJoiner result = new StringJoiner(System.lineSeparator());

        String input;
        while ((input = br.readLine()) != null) {
            final int n = Integer.parseInt(input);
            result.add(String.valueOf(computeAnswer(n)));
        }

        System.out.println(result);
    }

    private static int computeAnswer(int n) {
        long multiplyer = 1;
        int count = 1;

        while (multiplyer % n != 0) {
            multiplyer = multiplyer * 10 + 1;
            count++;
        }

        return count;
    }
}

하지만 이 코드는 시간초과로 실패했다. 이것 저것 시도를 해보다가 결국 포기하고 구글링을 했다.

이 문제는 아래의 나머지 성질을 이용해서 풀 수 있다.

(A + B) % C = (A % C + B % C) % C
(A * B) % C = ((A % C) * (B % C)) % C

이것은 수학 시간에 배우던 분배법칙과 비슷하다. 하지만 '%'라는 기호는 프로그래밍을 하면서 처음 알게되었고 증명이 필요했다.

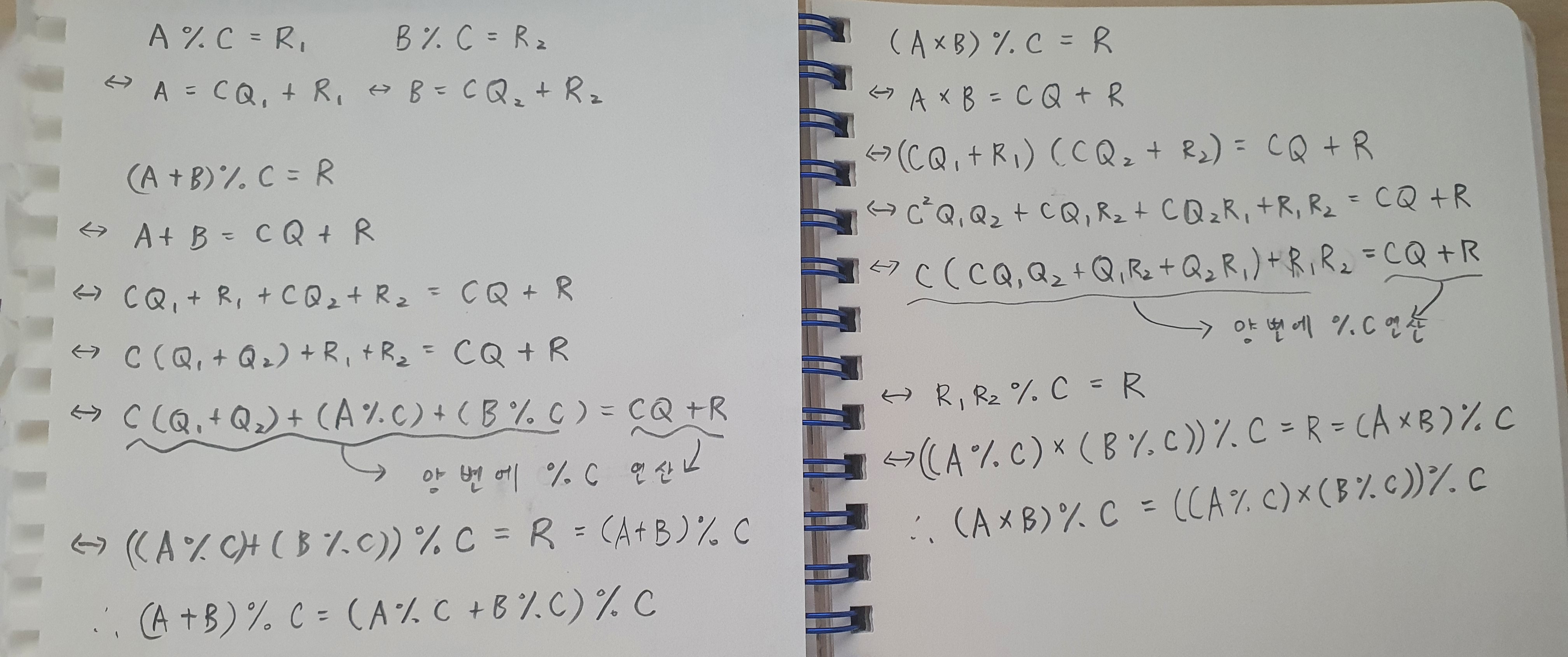
아... 근데 막상 이 공식을 통해서 어떻게 multiplyer = (multiplyer * 10 + 1) % n 으로 적용해도 된다는 걸 알 수 있는 건지 모르겠다. 아무리 봐도 모르겠네...ㅠ 내가 수학을 하는 건지 코딩을 하고 있는 건지...-_-;; 아무튼 그래서 더 간단한 방법으로 증명하는 건 불가능할까 고민하다가 아래와 같이 증명해봤다.

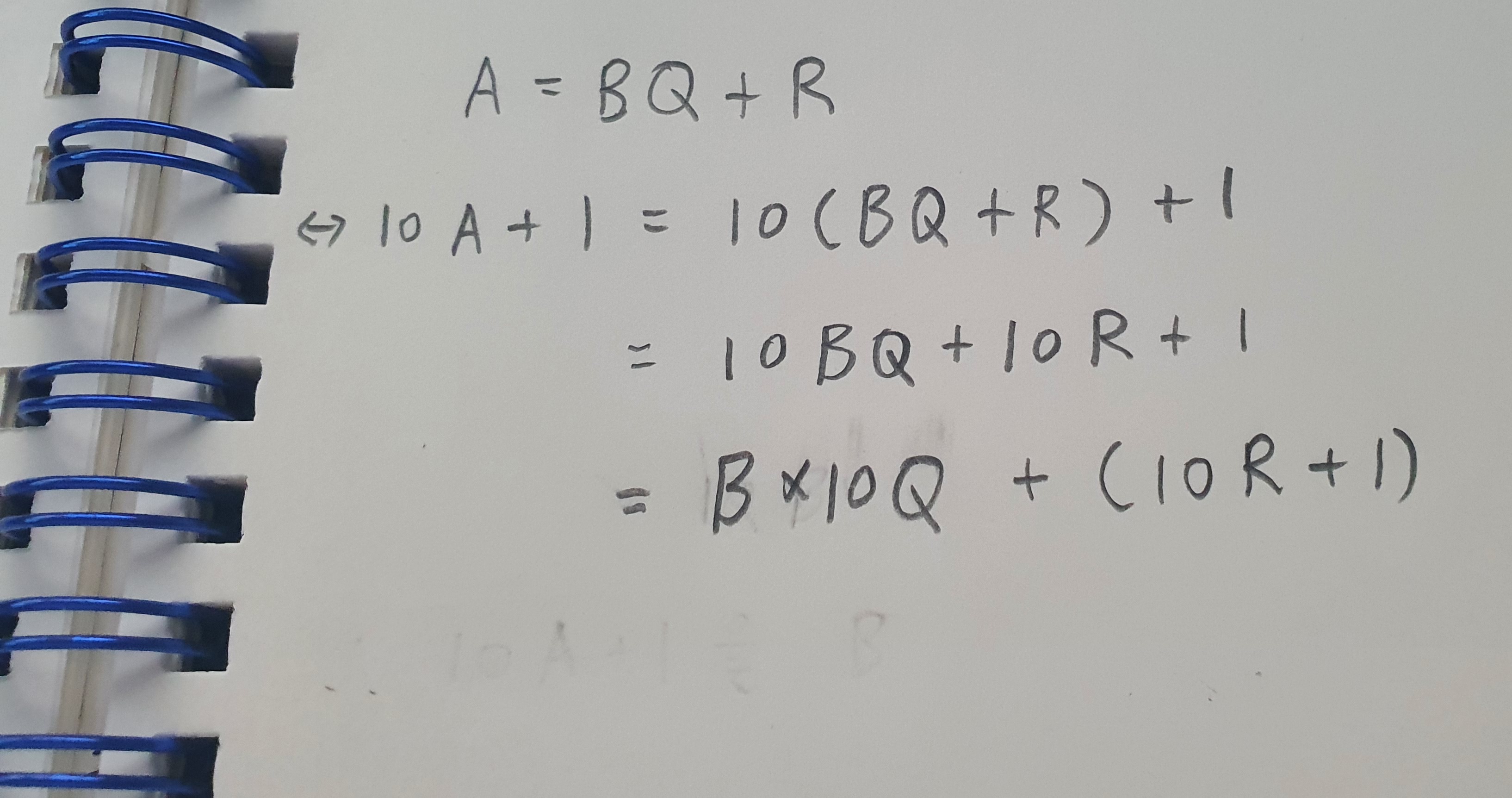
이렇게 하면, 10A + 1 을 B로 나눴을 때의 나머지가 10R + 1을 B로 나눴을 때의 나머지와 같다는 걸 쉽게 알 수 있다. 비단 10과 1에 국한되진 않을 거다. 아무튼 이 결과를 적용한 코드는 아래와 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringJoiner;

public class Main {
    public static void main(String[] args) throws IOException {
        final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        final StringJoiner result = new StringJoiner(System.lineSeparator());

        String input;
        while ((input = br.readLine()) != null) {
            final int n = Integer.parseInt(input);
            result.add(String.valueOf(computeAnswer(n)));
        }

        System.out.println(result);
    }

    private static int computeAnswer(int n) {
        int multiplyer = 1;
        int count = 1;

        while (multiplyer % n != 0) {
            multiplyer = (multiplyer * 10 + 1) % n;
            count++;
        }

        return count;
    }
}

이 문제를 통해 알게된 정말 놀라운 사실은, 기본형에 해당하는 수의 크기를 줄이는 것으로 속도를 향상시킬 수 있다는 것이었다. 연산에 드는 시간이 줄긴하겠지만, 이렇게나 차이가 날 줄이야...;

※ 참고 : https://dynamiccube.tistory.com/4

문제링크 : https://www.acmicpc.net/problem/1707

인접한 노드들을 모두 다른색(1과 -1)로 칠할 수 있는지의 여부를 체크해서 이분그래프인지 아닌지를 체크한다. 코드는 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int k = Integer.parseInt(br.readLine());
        StringBuffer sb = new StringBuffer();

        for (int i = 0; i < k; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int v = Integer.parseInt(st.nextToken());
            int e = Integer.parseInt(st.nextToken());

            @SuppressWarnings("unchecked")
            List<Integer>[] lists = new ArrayList[v + 1];
            int[] color = new int[v + 1];

            for (int j = 1; j <= v; j++) {
                lists[j] = new ArrayList<Integer>();
            }

            for (int j = 0; j < e; j++) {
                st = new StringTokenizer(br.readLine());
                int a = Integer.parseInt(st.nextToken());
                int b = Integer.parseInt(st.nextToken());

                lists[a].add(b);
                lists[b].add(a);
            }

            boolean bipartite = true;

            for (int j = 1; j <= v; j++) {
                if (color[j] == 0) {
                    if (!bfsCheck(lists, color, j)) {
                        bipartite = false;
                        break;
                    }
                    ;
                }
            }

            if (bipartite) {
                sb.append("YES\n");
            } else {
                sb.append("NO\n");
            }
        }

        System.out.println(sb);
    }

    private static boolean bfsCheck(List<Integer>[] lists, int[] color, int j) {
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.offer(j);
        color[j] = 1;

        while (!queue.isEmpty()) {
            int n = queue.poll();

            for (int elem : lists[n]) {
                if (color[elem] == 0) {
                    queue.offer(elem);
                    color[elem] = color[n] * -1;
                } else if (color[elem] != color[n] * -1) {
                    return false;
                }
            }
        }

        return true;
    }
}

문제링크 : https://www.acmicpc.net/problem/1167

트리의 지름을 구하는 문제다. 트리의 지름이란, 트리에서 가장 멀리 떨어져있는 두 노드 사이의 길이를 말한다.

트리의 지름을 구하는 방법은, 임의의 노드 x에서 DFS 백트래킹을 통해 가장 멀리 떨어져있는 노드 y를 구한 후, y에서 다시 DFS 백트래킹을 통해 가장 멀리 떨어져있는 노드 z를 구하면, y에서 z사이의 거리가 바로 트리의 지름이 된다. 이에 대한 증명을 해보자 -> (업데이트 예정)

코드는 아래와 같다.

문제링크 : https://www.acmicpc.net/problem/2873

필자가 싫어하는 그리디 유형이다...-_- 그리디 유형은 모든 경우의 수를 하나도 빠뜨림없이 고려하며, 각각의 경우의 수마다 규칙성을 찾고 그에 알맞게 코딩을 해야한다. 흐어... 그럼 설명을 시작해보도록 하겠다.

일단 연습장에 조금만 끄적여보다보면, 가로나 세로의 길이가 홀수일 경우, 모든 칸을 지나는 것이 가능하다는 것을 눈치챌 수 있을 것이다. 모든 칸을 지나갈 때의 점수보다 더 큰 점수를 만들 수는 없을 것이므로 이 때의 경로가 답이 된다. 그냥 지그재그로 움직이면 된다.

문제는 가로와 세로의 길이 모두 짝수일 때다. 이 때는 아무리 끄적거려봐도 모든 칸을 지나가는 것이 불가능하다. 조금 더 끄적거리다보면, 한 칸만 비워놓고 모든 칸을 지나가는 것은 가능하다는 것을 깨닫게 될 것이고, 빈 칸이 될 수 있는 칸은 아래 그림의 초록색 칸들이다.

초록색 칸은 i + j 가 홀수일 때다. 이 초록색 칸들 중에서 가장 낮은 점수를 가지고 있는 칸을 찾아서, 그 칸을 제외한 모든 칸을 지나가는 경로를 찾으면 점수가 최대인 경로를 얻게된다. 여기까지 생각해내는 건 쉽다. 이제 그 경로를 어떻게 찾아낼 수 있는지를 생각해내야하는데, 그게 좀 머리가 아프다...-_- 그 방법에 대해서는... 아래 코드를 보며 이해를 해보도록 하자^^;;;

문제링크 : https://www.acmicpc.net/problem/2579

필자는 이 문제의 출처가 정보올림피아드 '초등부'라는 걸 알았는데 꽤나 충격을 받았다... 난 초등학교 때 뭐했지...ㅠㅠ 각설하고, 설명을 해보도록 하겠다.

이 문제는 메모이제이션을 통한 다이나믹 프로그래밍 문제이다. 그렇다면 대체 무엇을 메모리에 남겨야할까?! 바로 각 계단까지 올라왔을 때의 점수의 최댓값이다. 코드는 아래와 같다.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

import java.io.BufferedReader; import java.io.InputStreamReader;   public class Main {     public static void main(String[] args) throws Exception {         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));         int n = Integer.parseInt(br.readLine());         int[] scores = new int[300];         int[] max = new int[300];                  for(int i = 0; i < n; i++) {             scores[i] = Integer.parseInt(br.readLine());         }                  max[0] = scores[0];         max[1] = scores[0] + scores[1];         max[2] = Math.max(scores[0], scores[1]) + scores[2];                  for(int i = 3; i < n; i++) {             max[i] = Math.max(max[i - 2], max[i - 3] + scores[i - 1]) + scores[i];         }                  System.out.println(max[n - 1]);     } } http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter

0, 1, 2 번째 계단까지 올라갔을 때 얻을 수 있는 최댓값에 대한 식은 다들 무리없이 이해할 수 있으리라고 본다. 그 다음 로직에 대해서 설명을 하면, i번째 계단에 오르기 위해선 i - 1번째 계단이나 i - 2번째 계단 둘 중 하나에서 올라와야한다. 두 가지 경우 중, 큰 값을 가지는 경우를 max값에 넣으면 된다. 근데 i - 1번째에서 올라올 경우, max[i - 1]의 값이 바로 i - 2번째 계단을 선택한 값인지 아닌지를 알 수가 없다. (i - 2번째 계단을 선택한 최댓값일 경우, i를 선택할 수 없으므로) 헌데 i번째, i - 1번째 계단 둘을 선택할 경우, i - 2번째 계단을 선택할 수는 없으므로 i - 3번째에서 왔을 것이다. 따라서 i - 1번째 계단에서 올라왔을 경우는 i - 1번째 계단의 점수와 i - 3번째 점수의 최댓값을 더하면 된다.

조금 다른 방식으로 풀 수도 있다. max를 2차원 배열로 선언하여, 바로 다음 계단을 선택할 수 있을 경우의 최댓값과 없는 경우의 최댓값을 저장하는 것이다. 코드는 아래와 같다.

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

import java.io.BufferedReader; import java.io.InputStreamReader;   public class Main {     public static void main(String[] args) throws Exception {         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));         int n = Integer.parseInt(br.readLine());         int[] scores = new int[300];         int[][] max = new int[2][300];                  for(int i = 0; i < n; i++) {             scores[i] = Integer.parseInt(br.readLine());         }                  max[0][0] = scores[0];         max[0][1] = scores[1];         max[1][1] = scores[0] + scores[1];                  for(int i = 2; i < n; i++) {             max[0][i] = Math.max(max[0][i - 2], max[1][i - 2]) + scores[i];             max[1][i] = max[0][i - 1] + scores[i];         }                  System.out.println(Math.max(max[0][n - 1], max[1][n - 1]));     } } http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter

 

문제링크 : https://www.acmicpc.net/problem/3108

거북이는 같은 선을 여러 번 그릴 수 있다. 따라서 교차하는 직사각형들을 한 그룹으로 보고(교차할 경우, 한 번에 다 그릴 수 있으므로) 그룹의 개수를 구하면 되는 문제이다.

위 그림을 예로 들면, 교차하는 직사각형의 그룹이 총 3개이므로, 로고는 총 3번의 PU 명령어를 통해 모든 직사각형을 그릴 수 있다.

교차하는 직사각형의 그룹의 개수를 구하는 방법은, 각 직사각형들이 교차하는 지의 여부를 인접행렬에 저장해놨다가 DFS를 통해 개수를 구한다. 코드는 아래와 같다.

여기서 조심해야할 것이 있는데, 직사각형 중 원점(0, 0)을 지나는 게 있는지의 여부이다. 하나라도 원점을 지나는 직사각형이 있을 경우, 거북이가 처음 PU명령어를 사용할 필요가 없어지므로, 이 때의 답은 '직사각형 그룹의 갯수 - 1'이 된다. 

그리고 두 직사각형이 교차하는 지의 여부를 구하는 조건이 좀 복잡하다;;

혹시 더 쉬운 방법을 아는 분은 댓글을 남겨주시면 감사하겠습니다.(굽신굽신)

문제링크 : https://www.acmicpc.net/problem/1525

필자는 이 문제를 풀 때 '메모리 제한 32MB'라고 써있는 걸 보고, 메모리를 아끼기 위해 최선을 다하며 풀었다. 근데 지금 생각해보면 자바의 경우 256MB로 그렇게 적은 편이 아닌데 굳이 그렇게까지 했어야했나 싶기도 하다^^; 메모리를 아끼기 위해 혼신(?)의 힘을 쏟으며 푼 코드는 아래와 같다.

전형적인 BFS문제이다. 메모리를 절약하기 위해 퍼즐의 상태를 2차원배열이 아닌, 정수로 변환해서 저장하는 것을 볼 수 있다. 또한 일반적으로 BFS를 풀 때는 방문여부(visited)를 boolean배열로 저장하지만, 이 경우에 boolean배열을 이용하려면 최소 876543211 크기의 배열을 선언해야하는데 대략 800MB정도 된다. 반면 Set으로 각각의 정수 값을 넣을 경우, 퍼즐에 배치될 수 있는 수의 모든 경우의 수가 9! = 362,880‬이기 때문에 훨씬 메모리를 절약할 수 있다. 그 밖에도 빈칸의 위치를 바꿀 때, char 배열로 잠깐 바꾼다음 swap하고 다시 정수로 바꾸면 편할텐데 메모리를 아끼기위해 계산을 통해 뽑아내는 눈물나는(?) 노력을 볼 수 있다ㅋㅋㅋ

문제링크 : https://www.acmicpc.net/problem/1107

낮은 정답률(현재 21%)에 비해 비교적 쉬운 문제다. 물론 필자도 처음 이 문제를 풀 때 엄청 헤맸다...;;; '아놔 그냥 리모컨 고쳐 쓰지 왜 망가진 걸 쓰고 난리야'라고 한탄하면서 풀었던 기억이 난다ㅋㅋㅋ 풀이에 대한 설명을 하자면

1. 망가지지 않은 버튼으로 누를 수 있는 채널 중 N과 가장 가까운, N보다 큰 값 upperNo를 구한다. 

   : 버튼을 누른 횟수 = upperNo의 길이 + (upperNo - N)

2. 망가지지 않은 버튼으로 누를 수 있는 채널 중 N과 가장 가까운, N보다 작은 값 lowerNo를 구한다.

   : 버튼을 누른 횟수 = lowerNo의 길이 + (N - lowerNo)

3. +, - 버튼으로만 이동

   : 버튼을 누른 횟수 = N - 100 의 절대값

이 3개의 값 중 가장 작은 값을 구하면 된다. 다들 여기까진 쉽게 생각을 할 것 같다. 문제는 1, 2번을 구하는 방법인데, 처음에는 어떻게든 규칙성을 찾으려고 발악을 했으나... 분기가 너무 많았다. 근데 생각을 해보자. 그냥 1씩 더하거나 빼면서 upperNo, lowerNo를 구할 때의 시간복잡도는 얼마일까? O(N)이다. 그냥 N... 아놔... 코드는 아래와같다.

몇 가지를 더 설명하자면, upperNo와 lowerNo가 절대 나올 수 없는 경우가 있다. 이 경우에는 아예 비교 대상에서 제외를 시켜야하는데, upperNo의 경우 1~9까지 모두 망가졌을 경우, lowerNo의 경우 모든 숫자 버튼이 망가졌을 경우에 나올 수 없다. 그 밖에도 N이 5인데 0~4까지 다 망가졌을 경우도 있을 수 있고 upperNo가 1,000,000보다 커질 경우에는 비교의 의미가 없다(N의 최대값이 500,000인데 +버튼만 이용해도 499,900번 누르면 갈 수 있기 때문)