문제링크 : https://www.acmicpc.net/problem/7453
7453번: 합이 0인 네 정수
문제 정수로 이루어진 크기가 같은 배열 A, B, C, D가 있다. A[a], B[b], C[c], D[d]의 합이 0인 (a, b, c, d) 쌍의 개수를 구하는 프로그램을 작성하시오. 입력 첫째 줄에 배열의 크기 n (1 ≤ n ≤ 4000)이 주어진다. 다음 n개 줄에는 A, B, C, D에 포함되는 정수가 공백으로 구분되어져서 주어진다. 배열에 들어있는 정수의 절댓값은 최대 228이다. 출력 합이 0이 되는 쌍의 개수를 출력한다. 예제 입력 1 복
www.acmicpc.net
이 문제에서 모든 경우의 수를 다 구해본다면, 그 때의 시간복잡도는 O(N^4)이다. N의 최댓값이 4000밖에 되지 않기 때문에 그렇게 푸는 것도 가능할 것 같긴 했으나(해보진 않음;;) 더 효율적인 방법을 알기에 그렇게 하지 않았다.
1. A와 B의 합, C와 D의 합에 대한 모든 경우의 수를 각각 subsetAB, subsetCD라는 새로운 배열에 저장한다. 이 때 각각의 subset의 크기는 N * N이 될 것이다.
2. 두 subset을 오름차순으로 정렬한다.
3. 두 subset의 합이 0일 때의 경우의 수를 센다. 이 때 투포인터 알고리즘을 사용한다.
투포인터 알고리즘에 대해 자세히 설명하면,
일단 left = 0, right = N * N - 1(subset의 가장 마지막 인덱스)로 초기화한다.
left는 subsetAB의 인덱스를 가리킬 것이고, right는 subsetCD의 인덱스를 가리킬 것이다.
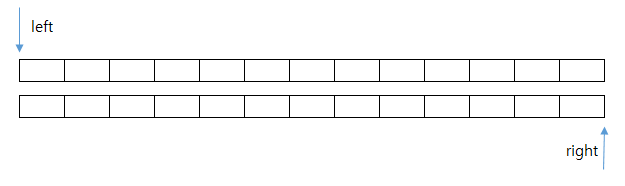
현재 각각의 subset은 오름차순으로 정렬되어있다. subsetAB[left] + subsetCD[right]의 값이 0보다 작다면 어떻게 해야할까? left를 증가시켜야한다. 현재의 subsetCD는 가장 큰값이므로 더 증가시킬수가없다. 반대의경우에는 right를 감소시키면된다. 이런식의 탐색을 통해 훨씬 적은 횟수의 비교를 통해 네 배열의 합이 0인 모든경우의수를 구할 수있다. 투포인터를 사용했을 시 시간복잡도는 O(N^2)이다. 코드는 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] a = new int[n];
int[] b = new int[n];
int[] c = new int[n];
int[] d = new int[n];
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
a[i] = Integer.parseInt(st.nextToken());
b[i] = Integer.parseInt(st.nextToken());
c[i] = Integer.parseInt(st.nextToken());
d[i] = Integer.parseInt(st.nextToken());
}
int[] subsetAB = getSubset(n, a, b);
int[] subsetCD = getSubset(n, c, d);
int left = 0;
int right = n * n - 1;
long cnt = 0;
while(left < n * n && right >= 0) {
int leftVal = subsetAB[left];
int rightVal = subsetCD[right];
int tmp = leftVal + rightVal;
if(tmp < 0) {
while(++left < n * n && subsetAB[left] == leftVal) {
// do nothing
}
} else if(tmp > 0) {
while(--right >= 0 && subsetCD[right] == rightVal) {
// do nothing
}
} else {
long leftCnt = 1;
long rightCnt = 1;
while(++left < n * n && subsetAB[left] == leftVal) {
leftCnt++;
}
while(--right >= 0 && subsetCD[right] == rightVal) {
rightCnt++;
}
cnt += leftCnt * rightCnt;
}
}
System.out.println(cnt);
}
private static int[] getSubset(int n, int[] a, int[] b) {
int[] subset = new int[n * n];
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
subset[i * n + j] = a[i] + b[j];
}
}
return subset;
}
}
|
cs |

'알고리즘' 카테고리의 다른 글
| 백준(BOJ) 11053 : 가장 긴 증가하는 부분 수열 (JAVA) (0) | 2020.02.11 |
|---|---|
| 백준(BOJ) 1451 : 직사각형으로 나누기 (JAVA) (0) | 2020.02.10 |
| 백준(BOJ) 1912 : 연속합 (JAVA) (0) | 2020.02.07 |
| 백준(BOJ) 11662 : 민호와 강호 (JAVA) (0) | 2020.02.07 |
| 백준(BOJ) 10816 : 숫자 카드 2 (JAVA) (2) | 2020.02.04 |