문제링크 : https://www.acmicpc.net/problem/3108
3108번: 로고
문제 로고는 주로 교육용에 쓰이는 프로그래밍 언어이다. 로고의 가장 큰 특징은 거북이 로봇인데, 사용자는 이 거북이 로봇을 움직이는 명령을 입력해 화면에 도형을 그릴 수 있다. 거북이는 위치와 각도로 표현할 수 있다. 거북이는 입에 연필을 물고 있는데, 연필을 내리면 움직일 때 화면에 선을 그리고, 올리면 선을 그리지 않고 그냥 지나가기만 한다. 제일 처음에 거북이는 (0,0)에 있고, 거북이가 보고 있는 방향은 y축이 증가하는 방향이다. 또한 연필은 내
www.acmicpc.net
거북이는 같은 선을 여러 번 그릴 수 있다. 따라서 교차하는 직사각형들을 한 그룹으로 보고(교차할 경우, 한 번에 다 그릴 수 있으므로) 그룹의 개수를 구하면 되는 문제이다.
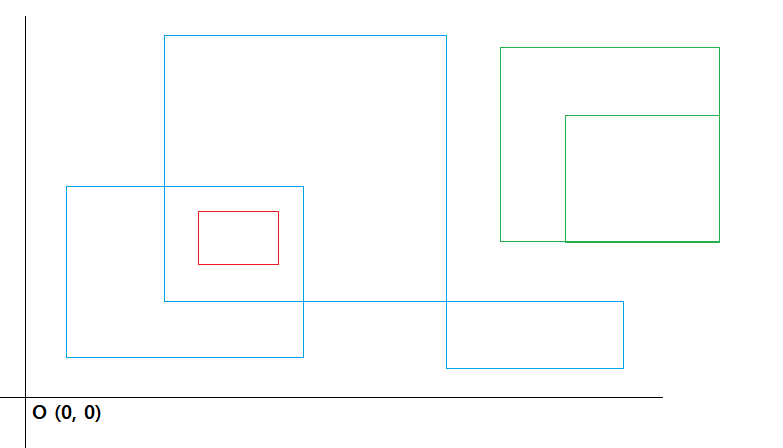
위 그림을 예로 들면, 교차하는 직사각형의 그룹이 총 3개이므로, 로고는 총 3번의 PU 명령어를 통해 모든 직사각형을 그릴 수 있다.
교차하는 직사각형의 그룹의 개수를 구하는 방법은, 각 직사각형들이 교차하는 지의 여부를 인접행렬에 저장해놨다가 DFS를 통해 개수를 구한다. 코드는 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
Rectangle[] rectangles = new Rectangle[n];
boolean[][] intersect = new boolean[n][n];
boolean crossZero = false;
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
rectangles[i] = new Rectangle(x1, y1, x2, y2);
if(y1 == 0 && x1 * x2 <= 0 || y2 == 0 && x1 * x2 <= 0 || x1 == 0 && y1 * y2 <= 0 || x2 == 0 && y1 * y2 <= 0) {
crossZero = true;
}
}
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(rectangles[i].intersect(rectangles[j])) {
intersect[i][j] = true;
}
}
}
boolean[] visited = new boolean[n];
int cnt = 0;
for(int i = 0; i < n; i++) {
if(!visited[i]) {
dfs(rectangles, intersect, visited, i, n);
cnt++;
}
}
if(crossZero) cnt--;
System.out.println(cnt);
}
private static void dfs(Rectangle[] rectangles, boolean[][] intersect, boolean[] visited, int i, int n) {
visited[i] = true;
for(int j = 0; j < n; j++) {
if(!visited[j] && intersect[i][j]) {
dfs(rectangles, intersect, visited, j, n);
}
}
}
private static class Rectangle {
private int x1;
private int y1;
private int x2;
private int y2;
public Rectangle(int x1, int y1, int x2, int y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
public int getX1() {
return x1;
}
public int getY1() {
return y1;
}
public int getX2() {
return x2;
}
public int getY2() {
return y2;
}
public boolean intersect(Rectangle rectangle) {
int _x1 = rectangle.getX1();
int _y1 = rectangle.getY1();
int _x2 = rectangle.getX2();
int _y2 = rectangle.getY2();
return !(_x2 < x1 || x2 < _x1 || _y2 < y1 || y2 < _y1 || (x1 < _x1 && x2 > _x2 && y1 < _y1 && y2 > _y2) || (_x1 < x1 && _x2 > x2 && _y1 < y1 && _y2 > y2));
}
}
}
http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter
|
여기서 조심해야할 것이 있는데, 직사각형 중 원점(0, 0)을 지나는 게 있는지의 여부이다. 하나라도 원점을 지나는 직사각형이 있을 경우, 거북이가 처음 PU명령어를 사용할 필요가 없어지므로, 이 때의 답은 '직사각형 그룹의 갯수 - 1'이 된다.
그리고 두 직사각형이 교차하는 지의 여부를 구하는 조건이 좀 복잡하다;;
혹시 더 쉬운 방법을 아는 분은 댓글을 남겨주시면 감사하겠습니다.(굽신굽신)

'알고리즘' 카테고리의 다른 글
| 백준(BOJ) 2873 : 롤러코스터 (JAVA) (0) | 2020.02.21 |
|---|---|
| 백준(BOJ) 2579 : 계단 오르기 (JAVA) (0) | 2020.02.18 |
| 백준(BOJ) 1525 : 퍼즐 (JAVA) (0) | 2020.02.14 |
| 백준(BOJ) 1107 : 리모컨 (JAVA) (0) | 2020.02.13 |
| 백준(BOJ) 2580 : 스도쿠 (JAVA) (0) | 2020.02.13 |